Eighth grade quadratic equations

Friends, today we all are going to learn the basic concept behind one of the most interesting and important topic of Grade VIII mathematics that is quadratic equations. Before proceeding further let's talk about Binomial formulas first. The Binomial formulas are:

(a + b)² = a² + b² + 2ab First Binomial formula

(a – b)² = a² + b² -2ab Second Binomial formula

(a² – b²) = (a + b)(a – b ) Third Binomial formula

Here a and b are the variables, or they can be even more general expressions. In the first and second binomial formulas, expression on the left are perfect squares while the expression on the left hand side of the third formula is the difference of two squares. One of the important thing to notice is that the first and second binomial formulas are equivalent. What student needs to do is to replace b with -b to get from one to the other.

We can use distributive law to verify the binomial formulas straight from left to right. For example:
(a + b)² = a(a + b) + b(a + b)
= a² + ab + ba + b²
= a² + 2ab + b²
Now I am going to discuss about quadratic equations. A polynomial equation of the second order is known as Quadratic equation. The general form of quadratic equation is:
ax² + bx + c = 0
where x is a variable and a, b and c are constants. Here a is quadratic coefficient, b is a linear coefficient and c is a constant term or we can say that it is a free term. To solve any quadratic problem or equation refers to find the value of variable. Let's take y that makes the equation true. To understand it better and in more deeply let's take an example:
(y – 1)² = 25
As we can say that it is not a quadratic equation, we can convert it into an equivalent equation that is in that form, by suitable operations on both the sides of the equation.

(y + 1)² = 25 expand
y² – 2y + 1 = 25
y² – 2y – 24 = 0 a = 1, b = -2, c = -24
The last solution or equation is in the standard form, where a, b and c having the given values.
But the second equation can be solved much more easily than the first one (ax² + bx + c = 0 ).
(y + 1)² = 25 root
y – 1 = ±5 +1
y = 1 ±5 consider both cases the answer
y = 6 or y = -4 (these are the two solutions of the equation.) Students needs to verify this by substituting these values in the exact equation. If y = 6 we get 5² = 25 and if y = 4
then we got (-5)² = 25.

Note the symbol ± in the above sequence of the equation. The square root value of the number 25 is positive by conventions and equals +5. Meanwhile, our task at that stage is not just evaluating a square root value as such, but our main focus should be there to answer the question for what values of y does (y – 1)² equal 25?
There are two such values y – 1 = -5 and y – 1 = + 5, and student needs to consider both the possibilities.
Now to understand it more wisely, consider the more general equation
(y – r)² = s (***)
where r and s are considered known and as before y need to be determined. The above equation can be solved just like we solve one before this.
Here r and s are considered known and as earlier y needs to be determined.
We can solve this in the same way as we can solve the above solved problem.
(y – r)² = s root
y – r = ±root s +r
y = r ±root s is the required answer

The most important way to solve a quadratic equation is to convert them to the above mentioned form. This process is known as completing the square. It is mainly based on the first and second binomial formulas.
Let's take an example to understand the basic concept behind and how this works with our equation in standard form:
y² – 2y – 24 = 0
If in the equation, the constant term was 1 instead of -24 than it would be a perfect square. To make it perfect square what we just need to do is add 25 on both the sides and get the desired value
y² – 2y + 1 = 25
It can be rewritten as
(y – 1)² = 25
Now the one thing is
(y – r)² = y² – 2yr + r²
What students need to do is to simply look at the factor of y, than halve it and in next step square it and in final step add the appropriate constant that makes the constant equal to that desired value. Another simplest of the way to find out that constant value is to subtract whatever constant is there and in final stage add the desired value. To solve it in this manner, work the leading coefficient (multiplying y²) must equal to 1. If it doesn't happen than we need to divide the first by the leading coefficient on both sides.
Now I am going to discuss about quadratic formula. Now what we need to know is what actually a quadratic formula is:
Take the standard form of the quadratic equation:

The general form of quadratic equation is:

ax² + bx + c = 0

where x is a variable and a, b and c are constants.

We already study that we can solve this general equation by completing the square exactly like we would solve it if the coefficients assumed specific values.

Quadratic equations can be solved by using following methods : factoring , completing the squares, graphing, Newton's method, and with the help of Quadratic formula.

The Quadratic formula. Quadratic equation is ax² + bx + c = 0 and it has the solutions

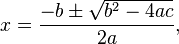here the expression under the square root sign is known as discriminant of the quadratic equation. Discriminant is denoted by the upper case Greek delta.

Delta = squared b – 4ac .

If the discriminant is zero then there is only one exact real root, also known as double root.

X = -b/2a.

The ‘±’ symbol indicate as ‘plus or minus’, which means that we need to work out the formula twice, once with a plus sign in that position, then again with a minus sign.

Clearly there are three cases while finding a discriminant:

D > 0 there are two real solutions

D = 0 there is one real solution

D < 0 there is a associated complex pair of solutions.

If you wants to apply the quadratic formula to a particular quadratic equation, what we need to do is just convert the equation to standard form and substitute the appropriate values of a, b and c in the formula. In between this is the more efficient and less error flat to make sure that student understand the binomial formulas and the basic concept behind completing the square and the most important is to solve a quadratic equation from scratch. In addition to these there are some of the formulas like the binomial formulas, the distributive law and different rules for manipulating powers, which needs to be remembered by the students.

Let's take an example to understand it better, we need to solve the following equation

x² - 4x - 5 = 0 , here no coefficient is written before x so we can use 1 as a coefficient of x. Now here a = 1, b = -4, and c = -5 now substitute this values in the above equation we get two values for the same that is x = 5 or x = -1.

The technique used for graphing quadratic equations is the same as for graphing linear equations. The most basic quadratic equation is y = x^2.. A quadratic graph is a parabola it can be generated by using quadratic math help calculator.

For solving quadratic equations we can also use math helper or solvers available over internet. For graphing quadratic equations we need to graph a proper parabola which is quite difficult , so we can use math helper which can provide us the useful x and y intercepts through which it becomes easy to graph a proper parabola of a particular quadratic equation.

Now in next class we all are moving forward and going to see the problems involving quadratic equations and try to solve them in a better and faster manner. In addition to these we are also going to understand the quadratic equation graphs.

How to tackle eighth standard Algebra

Friends we all know about Numbers and how to combine them using various operations like addition, subtraction, multiplication and division. This area of study is what we call as Arithmetic. The more advanced area of study of Algebra are distinct from arithmetic in which addition or basic operations to specific numbers involves entities, what we called as variables that have no particular value or we specify it as unknown value. Variables in common are generally denoted by upper or lower case letters. Some of the basic examples to show variables are “3a” , “x”, “ 7 + d” here a, x and d are variables having unknown values.

Let’s talk about algebraic expression in mathematics. An algebraic expressions is basically a collection of letters and numbers combined together to form an expression. These letters and numbers are combined together by the four basic arithmetic operations. Some of the examples of algebraic expressions are 7a, 7a + b, 7a – 4b, a / (a + b), a², (a + b)²
Here all the numbers used in algebraic expression are called constants and all the letters used in the above expressions like “a” and “b” are variables. If the expression comes with no variables then the algebraic expression is stated as arithmetic expressions. For example 4 + 7 / 6

Variables are generally used to explain the general situations or real time situations and they can also be used to solve problems that in anyway would be very difficult or even impossible to solve. Whenever we are going to solve algebraic expressions or any kind of word problems, we will see the use of these applications.

Now I am going to discuss about another topic which is very important that is an equation. In simplest mathematical manner we can say that an equation is an allegation in which two algebraic expressions used are equal. It is further stated in two different ways that are:
The first case: the given equation is true for all the values of the variables. In such kind of situation, equation is called an identity. The example to show an identity or we can say that values of variables which is true for the given equation. Most simple example is
x + y = y + x
It is also known as commutative law of addition. Another most common and well known identity is the first binomial formula or algebraic formulas like
(a + b)² = a² + 2ab + b²

The second case: In this situation the equation is true for some values of the variables. In such kind of problems or equations what we need to do is to identify those values of the variables for which the equation is true. This process is known as solving the equation. Moving forward we will study how to solve equations but for instance let’s take an example to understand the case in better manner
3a + 1 = 7
in this case obviously
a = 2 is the solution.

The given example is of a linear equation. We will further study about quadratic equations, but for know the example of a quadratic equation is a² – a – 2 = 0. If we are going to find out values for variables then, this equation has the two results that are:
a = -1 or a = 2

Now I am going in deep with the topic so the next topic is, How to evaluate an algebraic expression? To evaluate or to explore an algebraic expression refers to substitute or place specific values (desired values) for its variables. Let’s take a simple example of an algebraic expression to understand it better:
algebraic = 2a + 1

Now we are going to evaluate the given algebraic expressions. Now what we need to do is to try various values of variable which satisfy the given algebraic expression. Lets take a = 3, which provides us: algebraic = 2 x 3 + 1 = 7. we can say that the value of algebraic at a = 3 is 7. let’s take an example which is little tougher or  a bit complex then the above one
Now if we use above algebraic and put value of a = 2b + 1, where b is another variable which gives
Algebraic = 2 x (2b + 1) + 1 = 4b + 2 + 1 = 4b + 3
Now we can further solve this by substituting different values for variable b.

Before proceeding further towards inequalities let’s talk about equivalent expressions: Two expressions are equivalent if their values are equal for all possible evaluations of the two expressions. In other words presenting them with an equality sign between the expressions gives an identity.

Now I am going to talk about eighth grade linear equations topic:
In simple mathematical manner we can say that any equation that when graphed produces a straight line, then the equation is called as Linear Equation or we can say that any equation is a linear if it can be written in the linear form : ax = b. Here x is the variable, a and b are the constants. The common form of a linear equation in the two variables like x and y is
y = mx + b
where x and y are two variables and m and b are two constants.

The constant m determines the slope or gradient of that line and the constant b shows the point at which line crosses the Y-axis. Constant b is also known as Y-Intercept.
There are three possible solutions for the linear equations:
Unique Solutions: if a not equal to b then only possible solution: x = b/a
No Solution: If a = 0 and b is not equal to 0 then it has no solution.
Infinite Solutions or many solutions: if a = 0 and b = 0. In this solution 0x = 0 and there are infinite solutions for all the values of x.
Let’s take an example : 2a + 3 = a + 5
For solving this we need to subtract 3 from both the sides 2a = a + 2 that will result in a = 2.
The most important thing to understand is that, for solving a linear equation we need to recognize that the equation is linear or non linear and if linear then convert it to the simplest form. Lets take an example to elaborate it well:
(a – 2)(a – 3) = (a + 1)(a + 2)
what we need to do is to apply distributive property to both the sides of the equation
axa – ax3 – ax2 + 2x3 = axa + 2xa + 1xa + 1x2
on further simplifying this we get
a² – 5a + 6 = a² + 3a + 2
This is what we get, we can further simplify it by subtracting a² from both the sides.
Now after telling the basic concept behind linear equations, I am going to discuss about inequalities for class eighth. An inequality tells that two values are not equal. For example a ≠ b shows that a is not equal to b. The most important thing to understand is the use of inequality symbols. For solving inequalities we need to learn the symbols of inequalities like the symbol < means less than and the symbol > means greater than and the symbol ≤ less than or equal to etc.

In eighth standard we learn about linear inequality. So what linear inequality means is the first query comes in our mind. A linear inequality describes an area of the coordinate plane that has a boundary line. In simple way in linear inequalities everything on One side of a line on a graph. In mathematics a linear inequality is an inequality which involves a linear function.

The most important thing is to understand, how the inequality sign reverse when negative value comes. So to understand linear inequality, take an example: How to solve a compound inequality and graph the solutions?
Example: -6 < 2x - 4 < 12
-6 < 2x - 4 < 12
add 4 to all 3 parts
-2 < 2x <16
divide 2 from all 3 parts
-1 < x < 8
To graph the following equation, you put an open circle or we can say mark it by a dot on the point (-1,0) and then you put an open circle on the point (8,0).Then draw a line between the two.

We need to be careful while solving inequalities, as they are harder to solve than equations and require more attention. You can multiply an equation by a positive or negative number and get an equivalent equation. But while solving Inequalities remember this: when multiplying it by a negative number, you need to change sign of the inequality.