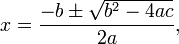Pythagoras Theorem in Grade VIII

Hello friends, in today's session we are going to learn about Pythagorean Theorem. This theorem is very useful and gives a very simple relationship between the three sides of a right angle triangle.

The theorem states that :

In any Right Angle Triangle, the area of the square whose Side is the Hypotenuse is equal to the sum of the areas of the square whose sides are the two legs. In algebraic form the theorem can be written as: a ² + b ² = c ², where a and b are the small sides and c is the hypotenuse of the right triangle.

In a right triangle if we know any two sides then we can easily find the other one with the Pythagoras equation.

If we generalize this theorem then we will get the law of cosines, which makes possible the computation of the third side of the triangle.

The converse of the theorem is also true:

For any three positive numbers a,b, and c such that a ² +b ² = c ², there exists a triangle with sides a,b and c, and every such triangle has a right angle between the sides of lengths a and b.

The Pythagoras equation can also be used to check what type of triangle we have, whether it is acute, obtuse or right angled. We can check this by using the following results:-

If a ² + b ² = c ², then the triangle is said to be right angled.

If a ² + b ² > c ², then the triangle is said to be acute angled.

If a ² + b ² < c ², then the triangle is said to be obtuse angled.

Pythagorean triplet is a set of three positive integers a, b and c, they are written in the form ( a, b, c). These triplets satisfy the Pythagoras equation a ² + b ² = c ².

For example - (3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37) are some among those which come below 100.

So let's solve some examples based on Pythagoras theorem.

1. if two sides of the triangles are 3 and 4, then find the length of the hypotenuse?

By using Pythagoras theorem. a ² + b ² = c ². in here a = 3 and b = 4, so the value of c will be c ² = 9 + 16.

c ² = 25

c = 5.

2. if one side of the triangle is 9 and the hypotenuse is 41, then find the other side.

In this problem a = 9 and c= 41, then the third side will be b.

b ² = c ² - b ^2.

b ² = 1681-81

b ² = 1600

b = 40.

3. check whether the triangle with given sides is a right triangle or not. a = 11, b = 60 and c = 61.

We can check whether it is a right triangle or not by using the Pythagoras theorem.

61² = 11² + 60^2.

3721 = 121 + 3600.

3721 = 3721,

so these three sides satisfy the Pythagoras theorem, so the triangle formed will be right angled.

Number System in Grade VIII

Hello friends, in today's session we are going to discuss about the Number System. The Number System is defined as a set of numbers arranged together in a such a manner so that we can perform different operations like addition, multiplication etc.

The number system is classified as follows:

1. Natural Numbers
2. Integers
3. Rational Numbers
4. Polynomials
5. Real Numbers
6. Complex numbers.

Let's just take them one by one and understand what are these:

Natural numbers is a set of all positive whole number greater than zero.

The set of natural numbers is denoted by N. There are various laws which the set of natural numbers follow:

Commutative axioms: a + b = b + a; a · b =b · a.

Associative axioms: a + (b + c) = (a + b) +c ; a · (b · c) = (a · b) · c.

Distributive axioms: a · (b +c ) = a · b +a · c; (b · c) n = b n · c n.

Identity axioms: a + 0 = a ; a · 1 = a ; a ⁰ = 1.

Now we come to Integers which are defined as for every natural number “a” there exists a Integer “-a” and the set of these numbers is represented by Z.

To perform arithmetic operations on integers we can look at generalizations given below to make our work simple.

−a + −b = −(a + b)

a + 0 = a

a − b = a + −b

−a · b = a · −b = −(a · b)

−a · −b = a · b

√4 can mean either 2 or −2.

The rational number system is a set of numbers used to represent the fractions. It allows the division to be done by all numbers except zero. It is written in the form a / b. where b cannot be equal to zero.

Polynomials are usually not called as numbers but their properties are very much similar to numbers.

Algebraic numbers is the system which includes all the rational numbers and is included in the set of real numbers.

The real numbers are those numbers which really exists. The set of real numbers is usually represented by R. Real numbers can also be defined as those ones which can be written in the decimal form. All the numbers we have studied till date are called as the real numbers, but now what are imaginary numbers. When the root of a  negative number is taken then the result is known as an imaginary number.

For Example – the number 24 is real because it can be written as 24.0. ½ is also a real number because it can be written as 0.5. even the number 1/3 is also real because it can be written as 0.3333.... whereas complex numbers or imaginary numbers are those numbers which are written in the form a + i b. where i is the imaginary unit i.e. a number whose square is minus one.

Tessellations in Grade VIII

Hii guys, so today we are going to study about a very new and different topic of Maths which is Tessellations. How many of you know what a Tessellations is? I believe not many but still a few might know. So let's start without wasting any time.

Tessellation is the process in which we create a two dimensional plane by repeatedly joining the geometric shapes without any overlaps and gaps. In simple language a tessellation is something in which we have some shapes and we join them together to form a regular sheet without any overlaps and gaps. We can see tessellations throughout our history, from ancient architecture to modern art.

For Example the Jigsaw puzzle we used to play when we were little. Its the best example we can get for our topic. It corresponds with the everyday term tiling which refers to applications of tessellations, often made of glazed clay. It also exist in the nature like the Honeycomb which also has a Tessellation structure.

For Example -

a tessellation of triangles

a tessellation of squares

a tessellation of hexagons

The above given figures are some examples of Tesselations, for more understanding.

Now let's study the different topics that comes under it.

When discussing about the tilings a form of tessellation, we see that they are multicolored, so we need to specify whether the colors are the part of tiling or just the part of an illustration.

Let's come to the theorem in our topic, it is known as the four color theorem.

The theorem states that every tessellation in every Euclidean plane, with a set of four available colors, each tiled when colored in one color such that no tiles of equal color meet at a curve of positive length. Note that the coloring guaranteed by the four-color theorem will not in general respect the symmetries of the tessellation. To produce a coloring which does, as many as seven colors may be needed.

Any arbitrary Quadrilateral when taken can also form a tessellation with 2-fold rotational centre at the mid point of all the four sides of the Quadrilateral. In a similar manner, we can construct a parallelogram subtended by a minimal set of translation vectors, starting from a rotational center. We can easily divide this by one diagonal, and take one half of the triangle as fundamental domain. Such a triangle formed will have the same area as of the quadrilateral and can be constructed from it by cutting and pasting.

Now we come over to the types of tessellations, we classify then in two types – the regular tessellation and irregular tessellation.

A regular tessellation is one which is highly symmetric and is made of congruent regular polygon. There are only three regular tessellations which exist. They are of Equilateral triangles, squares and regular hexagons. We even have a more accurate one which is edge-to-edge tessellation. In this type of tessellation the side of one polygon is fully shared with the sides of another polygon. There is no room for partial sharing of sides.

The most common example of the apperiodic pattern is the Penrose tilings which is formed using two different types of polygons and adds beauty to the walls. We also have the self dual tessellation and the example for it is the Honeycomb. Another example for it is shown in the figure below.

 

Tessellations is not only used in architecture but also to design the computer models. In the computer graphics, tessellation technique is used manage the datasets of polygons and divide them into polygon structure. This is generally used for rendering. The data is generally tessellated into triangles also known as triangulation.

The CAD application in our computers is generally represented in analytical 3D curves and surfaces.

The mesh of a surface is usually generated per individual faces and edges so that original limit vertices are included into mesh. The following three basic fundamentals for surface mesh generator are defined to ensure the approximation of the original surface that suits the need for the further processing

• The maximum allowed distance between the planar approximation polygon and the surface. This parameter ensures that mesh is similar enough to the original analytical surface (or the polyline is similar to the original curve).
• The maximum allowed size of the approximation polygon (for triangulations it can be maximum allowed length of triangle sides). This parameter ensures enough detail for further analysis.
• The maximum allowed angle between two adjacent approximation polygons (on the same face). This parameter ensures that even very small humps or hollows that can have significant effect to analysis will not disappear in mesh.

Some geodesic domes are designed by tessellating the sphere with triangles that are as close to equilateral triangles as possible.

So as we have read above that a honeycomb is a natural tessellation, there are some more tessellations in our nature like when the lava flows, it often displays columnar jointing, due to the contraction forces that are present, it causes the lava to break into cracks when it is cooled. These cracks often gets broken in the hexagonal columns. The tessellation is even present in the flower petals, leaves, tree bark, or a fruit. It is not easily visible but when we look through the leaf etc. with the help of a microscope then we can easily see the formation.

It seems like what we have learned till now seems to be theoretical, so let's now have something mathematical in it.

Now the topic that comes under it is, Number of Sides of a Polygon versus the number of Sides at a Vertex.

If we assume an infinite long tiling, then let a be the number of sides of a polygon and b be the average number of sides which meet at the vertex. Then ( a – 2 ) ( b – 2 ) = 4. For example, we have the combinations (3, 6), (31/3, 5), (33/4, 42/7), (4, 4), (6, 3) for the tilings.

For a tiling which repeats itself, one can take the averages over the repeating part. In the general case the averages are taken as the limits for a region expanding to the whole plane. In cases like an infinite row of tiles, or tiles getting smaller and smaller outwardly, the outside is not negligible and should also be counted as a tile while taking the limit. In extreme cases the limits may not exist, or depend on how the region is expanded to infinity.

For a finite tessellation and a polyhedra we have

( a – 2 ) ( b – 2 ) = 4 (1 – X/f ) ( 1 – X/v ).

In this expression f represents the number of faces of a polygon and v represents the number of vertex and X is the euler characterstic.

The formula follows observing that the number of sides of a face, summed over all faces, gives twice the total number of sides in the entire tessellation, which can be expressed in terms of the number of faces and the number of vertices. Similarly the number of sides at a vertex, summed over all vertices, also gives twice the total number of sides. From the two results the formula readily follows.

In most cases the number of sides of a face is the same as the number of vertices of a face, and the number of sides meeting at a vertex is the same as the number of faces meeting at a vertex. However, in a case like two square faces touching at a corner, the number of sides of the outer face is 8, so if the number of vertices is counted the common corner has to be counted twice. Similarly the number of sides meeting at that corner is 4, so if the number of faces at that corner is counted the face meeting the corner twice has to be counted twice.

A tile with a hole, filled with one or more tiles is not permissible, because the network of all sides inside and outside is disconnected. However it is allowed with a cut so that the tile with the hole touches itself. For counting the number of sides of this tile, the cut should be counted twice.

The another topic that we are going to study is the Tessellation of other spaces. As well as tessellating the 2-dimensional Euclidean plane, it is also possible to tessellate other n-dimensional spaces by filling them with n-dimensional polytopes. Tessellations of other spaces are often referred to as honeycombs.

So this is all we have for the topic tessellations and I hope that you would have understood what a tessellation is. This topic we have learned is totally a theoretical one, but it do have some problems to do, and I expect that you will be able to understand how to solve them by using the only formula which we have learned so far in this topic.

Quadratic Equation in VIII Grade

Hello friends, in today's class we are going to learn what a quadratic equation is and how can we solve it.

 

A Quadratic equation is a second order univariate polynomial equation. A general quadratic equation can be written as a x² + b x + c, here x is the variable and a,b and c are the constants with a ≠ 0. There are two solutions of the quadratic equations, either both are real or both are complex.

There are various methods of solving quadratic equations but the ones that we have to learn are as follows-

1. factoring
2. completing the square
3. by using the quadratic formula.

Let's start solving the quadratic equations by using the above methods one by one.

 

We start by using the factoring method, let's understand by using the general formula.

The general equation is ax² + bx + c. We follow some general steps to solve the quadratc equation.

1.multiply the constants a and c without forgetting their signs.

2.Write down b, with its sign.

3.Write all the possible factors of the products of ac and find which pairs add up to give b.

4.Now rewrite the x terms as the sum of two terms with these selected numbers as the coefficients.

So by this we can find the solution of any quadratic equation.

For Example –

1. Solve x² + 5 x + 6.

Answer – the possible combination of the middle term is 1x+4x and 2x+3x.

The product of a and c is 6 x 1= 6. So the second combination is the suitable option for this quadratic expression. So now it can be written as x² + 3 x + 2 x + 6.

Now we take x common from the first two terms and 2 from the last two terms.

Now the quadratic equation becomes x ( x + 3 ) + 2 ( x + 3 ).

This time we take (x + 3) common, so the equation now becomes (x + 2 ) ( x+ 3 ).

the value of x = -3, -2.

The solution for the quadratic equation x² + 5 x + 6 is x = -2, -3.

2. Solve x² – 3 = 2 x.

We bring 2x on the left hand side. So now the equation is x² – 2 x – 3.

now breaking the middle term we see that the possible combination is -1x -1x and -3x + x.

The product of a and c is -3. So the second combination is the suitable one for this quadratic expression.

Now the equation becomes x² – 3 x + 1 x – 3.

now by taking x common from the first two terms and 1 from the last two terms we get,

x ( x – 3 ) + 1 ( x – 3 ). Now taking x - 3 common from both the terms. We get

(x + 1 ) ( x – 3 ).

x = -1, 3.

so the solution to the quadratic equation x² - 2 x – 3 is x = -1, 3.

3. Solve x² - 9.

Answer- we can see that it is in a² - b² form, so we can break it as ( a + b )( a – b ).

So our equation becomes ( x + 3 ) ( x – 3 ).

now x = -3 , 3.

So the solution to the quadratic equation x² - 9 is x = -3, 3.

 

2. By completing the squares.

For the general equation a x² + b x + c.

In this method we follow these steps.

1. take the constant to one side and make the coefficient of x² = 1.
   

2. add the square of the half of coefficient of x on both the sides in the expression as shown above.
Now we can easily find out the value of x.
Let's clear the doubts with the help of an example.
1. Solve x² - 5 x + 6.
we follow the same general steps.
= x² - 5 x = -6.
add the square of the half of coefficient of x on both sides.
= x² - 5 x + 25/4 = 25/4 – 6.
so the left hand side becomes
= (x - 5/2)² = 25/4 – 6.
= (x – 5/2) = ± ¼.
Now value of x = 5/2 + ¼ or 5/2 – ¼.
x = 3, 2.
2. Solve x² – 3 = 2 x.
= x² - 2 x = 3.
= x² - 2 x + 1 = 3+1.
= (x -1)² = 4.
= (x -1) = ± 2.
= x = 1+ 2 or 1-2.
= x = 3, -1.
3. solve x² - 9.
In this we can see that the coefficient of x = 0, so we bring the constant to the right hand side.
= x² = 9.
= x = ± 3
= x = -3, +3.
Let's now use the third method to find the solution to the quadratic expressions that is by using the quadratic formula.


3. For the general equation a x² + b x + c.

The value of


The two values are using the positive and the negative signs.
But how did we got this formula?
We got this by using completing the squares method, which we have just learned.
Let's derive it for our general equation,
1.


2.


3.



4.






So this is how we got our general formula. Let's now solve some questions using this quadratic formula.
1. Solve – .




Here a = 2, b = -3 and c = 1/2. now we put these values in the formula and find the values of x.




So we get two values of x.
2. Solve-

for x by using the quadratic formula. Here a = 1, b = 2 and c = 10 .

so we put these values in the formula.

So the value of x becomes,

 

Now as we have solved the quadratic equations by using the different methods, so let's now solve some word problems on Quadratic equations.

By using the same general formulas we can solve the word problems on quadratic equations, What we have to do is just form the quadratic expression from the given problem and the rest could be found using the above three formulas.

Let's solve some of them for more understanding.

 

1. Question - The length of a rectangle is 6 inches more than its width. The area of the rectangle is 91 square inches. Find the dimensions of the rectangle.

Answer - The formula for the area of a rectangle is length x breadth.

So if width is assumed as x than the other side i.e. the breadth will be x+6 as per the given condition.

So the area is x ( x + 6 ), and the area is given as 91.

So x ( x + 6 ) = 91.

now the quadratic equation is x² + 6 x – 91 = 0.

so now by solving this equation we will get x = 7, -13.

since the length of the triangle cannot be negative so the breadth of the triangle is 7 and its length is 7 + 6 = 13.

2. Question - The product of two consecutive odd integers is 1 less than four times their sum. Find the two integers?

Answer – let us assume the first number to be n. Since the second number is the consecutive odd one so the value of second number will be n + 2.

now we implement the given problem.

The product of two numbers will be n(n+2), this is equal to 1 less than 4 times its sum,

the sum is 2 n + 2, 4 time of it 4 x (2 n + 2 ), and it is 1 less = 4 ( 2 n + 2 ) -1.

so the final quadratic equation is n² + 2 n = 8 n + 8 – 1.

= n² - 6 n – 7.

By solving the above quadratic equation we get the values of x as 7, 9 and -1, 1.

So these are the two possible combinations possible for the numbers.

3. Question-The hypotenuse of a right triangle is 6 more than the shorter leg. The longer leg is three more than the shorter leg. Find the length of the shorter leg.

Answer – for solving these equations we should know about pythagoras theorem.

According to pythagoras theorem (side)² + (side)² = (hypotenuse)²

Take one side as x, than the other side is x + 3 and the hypotenuse is x + 6.

now by using the pythagoras theorem.

x² + ( x + 3 )² = ( x + 6 )²

so we get, x² - 6 x – 27.

now by solving this we will get x = -3, 9. since the side cannot be negative so the value of will be 9.

Variables in VIII Grade

Hello friends in today's session we are going to learn about variables, expressions, equations and inequalities. Let's just take them one by one. We will start with variables.

A variable in mathematics is a quantity which may change itself according to the given conditions. It is generally represented by English alphabets x, y z, a, b, c etc. If the given condition has no variables than it is said to have constants.

A constant is a value which remains unchanged like numbers 3, 4, 5 etc.

For Example- x + 2 = 6, where x is variable and 2,6 are constants.

Variables are further categorized as dependent and independent variables.

The variables whose value depend on other terms in the condition are known as the dependent variables whereas the ones which take different values freely are known as the independent variables.

When variables come together with some constants then they form an expression. Like y = f(x) is a general expression. This equation says that y is a function of x, so the variable x is an independent variable and the variable y is dependent on x.

y = f(a, b, c), here also y is a function of a,b and c. So the variable y is dependent whereas a, b and c are independent variables.

Now the expression properly is a mathematical term which uses variables and the constants with different mathematical operations.

Example-

x

2

x + 2

y + 8

x + y

2x + 9z etc.

Now we move towards the equations.

An equation is an expression which is equal to some other constant or variable. Equations are used to find the values of the given variables. The word problems in the maths are generally solved by forming equations.

For Example-

2 = 2

17 = 2 + 15

x = 7

7 = x

t + 3 = 8

3 × n +12 = 100

are the equations.

Now since we know what an equation is, so we now will try solving the given equation.

This is done by two methods either by solving the given equation to bring the value of the variable or by substituting the different values of variable that is the hit and trial method.

For Example

Solve 4z + 12 ?

this we will done by solving for z that is the first method.

To make it easy we use some general steps.

Step 1- simplify the equation to bring it in the simplest form.

The given equation is already in its simplest form.

Step 2- equate the give equation to 0 by bringing all the terms to one side .

4z + 12 = 0.

Step 3 – bring the constants on one side and leave the variables on the other side.

4z= - 12.

Step 4 – make the coefficient of the variable equal to 1.

in this case we will divide the equation by 4.

4z/4 = -12/ 4 , so our equation becomes

z = -3 .

so the result after solving 4z +12 = 0 is z = - 3.

This method though is very easy for small problems but becomes very difficult for complex problems.

So we use the hit and trial method for complex problems

For Example-

Solve 4z + 12 = 0 ?

we substitute different values of z and see if it becomes equal to 0.

so put the value of z = 0

= 12= 0

which is not possible.

So we put 1

4+12 = 0

16 = 0 which is also not possible.

Now for z = -1

- 4 + 12 = 0

8 = 0

which is also not possible.

Now we put z = - 3

so

4 x – 3 + 12 = 0

-12 + 12 = 0

0=0

so this the answer for the above gives equation.

Now you will be having one question in your mind that how will you know that which value it will satisfy and how many times we will have to perform this method.

So that is the reason we generally used the first method, and avoid the hit and trial method. The method is only used when the equations formed by the first method becomes very complex.

Let's solve some word problems.

1. The sum of my age and 20 equals 40

to solve this problem, we will first form an equation. Let my age be x, so according to the problem

x + 20, that is the sum of my age plus 20, and this is equal to 40

so the equation is x + 20 = 40 .

so now by using the steps for solving a given equation. We see that the value of x = 20.

2. The difference between my age and my younger sister's age, who is 11 years old, is 5 years.

So in this problem let my age by y, my sister's age is 11 and the difference between our age is 5.

y – 11 = 5 is the equation.

Now by solving the equation by the general steps.

We get the value of y = 6.

so my age is 16.

What we have learned about the equations till now is all about the linear equations that is the equations with exponent as 1.

Now we move to the quadratic equations, those equations which have 2 as their variable powers are known as the quadratic equation. We have to keep one thing in mind before solving the equation and it is that if the equation is linear then there will be one solution for the variable, if quadratic then 2 solutions, if three than 3 solutions and so on.

For Example.

is a Quadratic equation.

The quadratic equation is solved by using a general formula known as the quadratic formula.

This is the general formula that we use to solve the quadratic equations. Now the two solutions will be

Let's now solve some problems on quadratic equations.

For Example

Solve x² + 5x + 6 = 0.

we use the quadratic formula to solve the above equation.

Here a = 1, b= 5 and c = 6.

so we will put it in the formula and get two values of x.

after solving the values x comes out to -2 and -3.

Now we move to the inequalities.

Inequality is used to compare the two sides of the given equation. It is represented by using two symbols, “<” for less than and “>” for greater than. Let's understand this with the help of some notations.

x < y = this means that x is lesser than y.

x > y = this means that x is greater than y.

The other notations used are

1. ≤ for less than or equal to.
2. ≥ for greater than or equal to.
3. ≠ for not equal to.
4. <<much lesser than.
5. >> much greater than.

These notations are not used very commonly, but they do sometimes come in the questions.

There are some properties of inequalities that we need to know.

1. transitivity .

If a > b and b > c then we can say that a > c. Or we can write it as if a < b and b < c than a < c.

2. addition and subtraction property.

If a < b then, a + c < b + c or a – c < b – c.

3. for multiplication.

If a < b then, ac < bc or a/c < b/c.

4. the inverse property.

If a < b then -a > -b.

if a > b then -a < -b.

5. the multiplication inverse.

If a < b then 1/a > 1/b. And if a > b then 1/a < 1/b.

The inequalities are generally solved graphically.

For Example.

1.Solve x + 3 < 2 ?

so we solve the inequality by taking the constant on one side and variables on the other.

= x < -1

so this is the answer for the equation.

This tells us that all the region from -1 to negative infinity is the answer.

2.. solve 2 – x > 0.

for this we will use same procedure.

Which gives x < 2

So all the region from 2 to negative infinity is the answer.

3. Solve: -2y <-8 ?

so by using the reversing property, the equation becomes.

2y > 8

y > 4.

This tells that all the region above 4 is the answer.

We can plot this one also like the others.

Now moving towards much more complex examples.

4. Solve -2 < (6-2x)/3 < 4?

we can see that in this we have two inequalities at the same time.

We will solve it by taking one inequality at a time.

So now we have two inequalities that is, -6< 6 – 2 x and 6 – 2 x < 12.

Solving the fist one we get the answer for x < 6 and the second inequality gives us x > -3.

so the final answer is -3 < x < 6.

So that's all for today and I hope that you will have no problem in solving any of the questions from Variables, expressions, equations and inequalities.